Curso de Máximo Divisor Comum (MDC)

Revise este importante conteúdo de matemática.

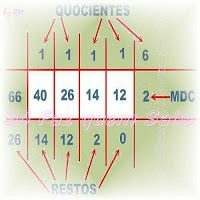
O Máximo Divisor Comum (MDC) é um assunto considerado muito importante dentro da matemática. O MDC pode ser considerado como o produto dos divisores comuns entre dois ou mais números inteiros. Os números divisores são aqueles que ocorrem quando o resto da divisão é igual a zero. Por exemplo, o número 12 é divisível por 1, 2, 3, 4, 6 e 12. Se dividirmos 12 por esses números obteremos um resultado exato, sem que haja um resto na divisão.

Quando um número tem apenas dois divisores, ou seja, ele é divisível somente por 1 e por ele mesmo, eles são chamados de números primos. Vale notar que todo número natural possui divisores. O menor divisor de um número será sempre o número 1. Por sua vez, o maior divisor de um número é o próprio número.

Aprenda mais sobre o MDC neste curso de matemática online e gratuito. Não deixe de conferir também o curso de Matemática para Concurso Público.

Sobre o curso

Neste curso online e gratuito os alunos poderão revisar a teoria por trás do Máximo Divisor Comum. O curso é recomendado especialmente para estudantes do nível médio que tenham interesse em estudar matemática e se preparar para provas ou afins.

Estrutura do curso

Grings – MDC – Máximo Divisor Comum – ( Aula 1 )

Grings – Exercícios de Aplicação do Máximo Divisor Comum – MDC – ( Aula 2 )

Grings – Exercícios de Aplicação do Máximo Divisor Comum – MDC – ( Aula 3 )

Grings – Exercício de Máximo Divisor Comum – MDC – ( Aula 4 )

Grings – Exercícios de Aplicação do Máximo Divisor Comum – MDC – ( Aula 5)

Grings – Máximo Divisor Comum – MDC de Números Grandes – ( Aula 6)

Grings – Máximo Divisor Comum com Fatoração de Números Primos – ( Aula 7)

Grings – Máximo Divisor Comum: Questão de Concurso ( MDC ) – ( Aula 8)

Grings – Aplicações do Máximo Divisor Comum ( MDC ) – ( Aula 9)

GRINGS – Máximo Divisor Comum – Exercício Clássico ( MDC ) – ( Aula 10)

Grings – Máximo Divisor Comum – Cercando Terreno – ( MDC ) – ( Aula 11)

Grings – Máximo Divisor Comum – Sobre Volume – ( MDC ) – ( Aula 12)

Grings – Máximo Divisor Comum – Divisão com Resto – ( MDC ) – ( Aula 13)

GRINGS – Máximo Divisor Comum – Algoritmo de Euclides – ( MDC ) – ( Aula 14)

GRINGS – ( MDC ) – Algoritmo de Euclides para Três Números – ( Aula 15)

GRINGS – ( MDC ) – Algoritmo de Euclides Questão de concurso – ( Aula 16)

GRINGS – ( MDC ) – Três Maneiras Diferentes para achar Máximo Divisor Comum – ( Aula 17)